Tärkein ero: Matriisi tai matriisit ovat suorakulmainen ruutu numeroista tai symboleista, jotka on esitetty rivi- ja sarakemuodossa. Determinantti on neliömatriisin komponentti, eikä sitä voida löytää missään muussa matriisityypissä.
Matriisit ja determinantit ovat tärkeitä lineaarisen matematiikan käsitteitä. Näillä käsitteillä on suuri merkitys lineaarisissa yhtälöissä, joita voidaan soveltaa myös fysiikan, mekaniikan, optiikan jne. Todellisten ongelmien ratkaisemiseen. Matriisi on rivi-, sarake- tai sarakemuotoinen järjestys. Määrittäjä on numero, joka liittyy neliömatriisiin. Nämä kaksi termiä voivat olla melko hämmentäviä ihmisille, jotka vain oppivat näitä käsitteitä. Yritetään ymmärtää ne erikseen.
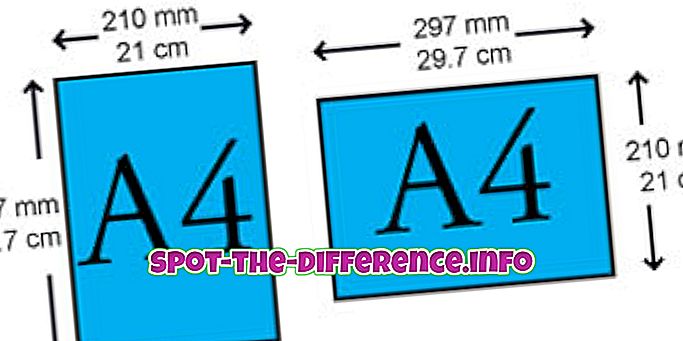
Matriisi on suorakulmainen ruutu numeroista tai symboleista, jotka on esitetty rivi- ja sarakemuodossa. Matriisin jokainen yksittäinen termi tunnetaan elementteinä tai merkinnöinä. Matriisi määritetään rivien ja sarakkeiden lukumäärällä. Esimerkiksi matriisia, jossa on 2 riviä ja 3 saraketta, kutsutaan 2 x 3 -matriisiksi. Matriisilla voi olla myös parillinen määrä rivejä ja sarakkeita; näitä kutsutaan neliömatriisiksi. Muita matriisin muotoja ovat: rivivektori ja pylväsvektori. Rivivektori on matriisi, joka koostuu vain yhdestä numerorivistä, kun taas sarakevektori on matriisi, joka koostuu vain yhdestä sarakkeesta.
Matriisit on yleensä suljettu nelikulmaisiin tai kaareviin kiinnikkeisiin. Jokainen suljettu pidike on yksi matriisi. Näille matriiseille on osoitettu pääomakirjain, joka edustaa matriisia. Matriisissa olevat tiedot voivat olla minkä tahansa tyyppisiä numeroita, mukaan lukien positiiviset, negatiiviset, nolla, fraktiot, desimaalit, symbolit, aakkoset jne. Matriiseja voidaan lisätä, vähentää tai kertoa. Jos kyseessä on kahden matriisin lisääminen, vähentäminen ja kertominen, matriiseissa on oltava sama määrä rivejä ja sarakkeita. Useita kertoja on kaksi: skalaarinen kertominen ja matriisin kertominen toisella matriisilla. Scalar-matriisiin sisältyy matriisin kertominen yhdellä numerolla.

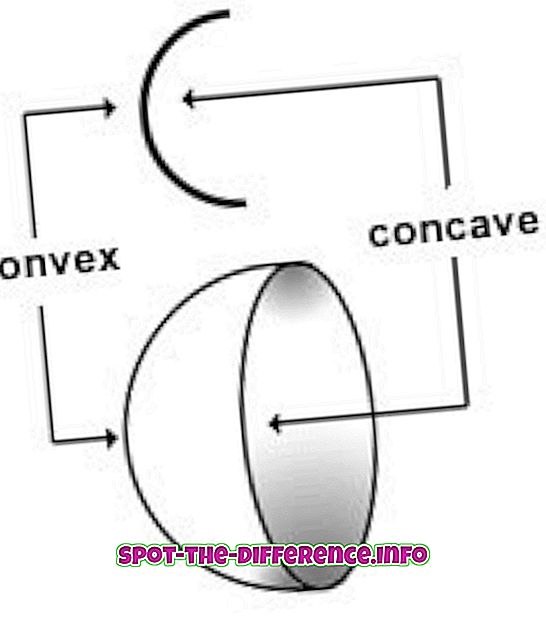
Kahden matriisin moninkertaistaminen keskenään edellyttää niiden ratkaisemista "pistetuotteessa", jossa yksi rivi kerrotaan yhdellä sarakkeella. Tuloksena olevat luvut lisätään sitten. Ensimmäisen kertomuksen tulos olisi 1 x 7 + 2 x 9 + 3 x 11 = 58.

Matriiseja on erilaisia: neliö, diagonaali ja identiteetti. Neliömatriisi on matriisi, jolla on sama määrä rivejä ja sarakkeita eli 2x2, 3x3, 4x4 jne. Diagonaalimatriisi on neliömatriisi, jossa on nollia elementteinä kaikissa paikoissa, paitsi diagonaaliviivassa, joka kulkee diagonaaliviivasta, joka kulkee ylhäällä vasemmalta oikealle. Identiteettimatriisi on diagonaalimatriisi, jonka kaikki diagonaalielementit ovat yhtä suuret kuin 1.
Matriiseja käytetään näkyvästi lineaarisessa muunnoksessa, jota tarvitaan lineaaristen toimintojen ratkaisemiseen. Muut kentät, jotka sisältävät matriiseja, ovat klassinen mekaniikka, optiikka, sähkömagneettisuus, kvanttimekaniikka ja kvanttielektrodynamiikka. Sitä käytetään myös tietokoneohjelmoinnissa, grafiikassa ja muissa tietojenkäsittelyalgoritmeissa.
Determinantti on neliömatriisin komponentti, eikä sitä voida löytää missään muussa matriisityypissä. Määrittäjä on todellinen luku, jota voidaan epävirallisesti pitää neliömatriisin ratkaisun tuloksena. Määritys määritetään det (matriisi A) tai | A |. Se voi tuntua A: n absoluuttiselta arvolta, mutta tässä tapauksessa se viittaa matriisin A determinanttiin. Neliön matriisin determinantti on päädiagonaalin elementtien tuote, josta on vähennetty päädiagonaalista elementtejä.
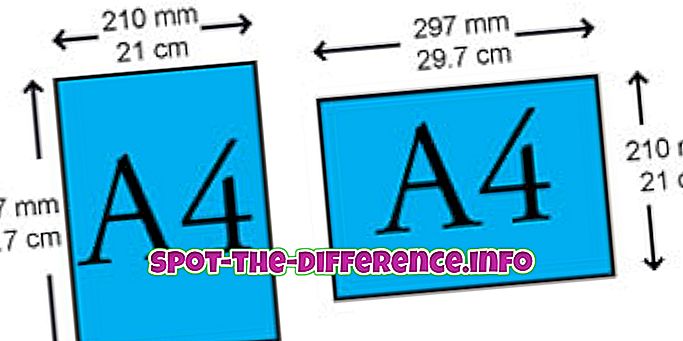
Oletetaan esimerkki matriisista B:

Matriisin B tai | B | olisi 4 x 6 - 6 x3. Tämä antaisi determinantille 6.
3x3-matriisissa käytettäisiin samanlaista kuviota.


Richland Community College -koulutussivustolla todetaan, että tekijöillä on erilaisia ominaisuuksia:
- Määrittäjä on todellinen luku, se ei ole matriisi.
- Determinantti voi olla negatiivinen luku.
- Se ei liity absoluuttiseen arvoon ollenkaan, paitsi että molemmat käyttävät pystysuoria viivoja.
- Determinantti on olemassa vain neliömatriiseille (2 × 2, 3 × 3, ... n × n). 1 × 1 -matriisin determinantti on se, että determinantin yksittäinen arvo.
- Matriisin käänteinen suuntaus on olemassa vain, jos determinantti ei ole nolla.