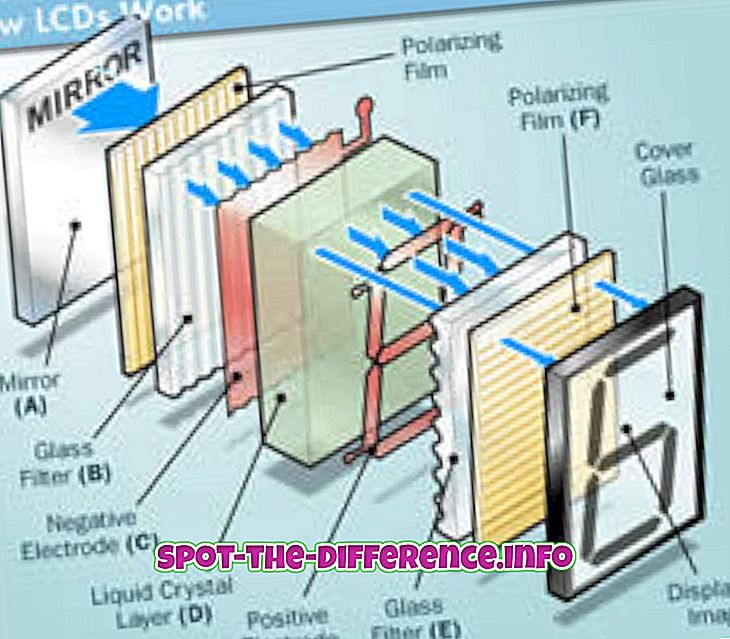
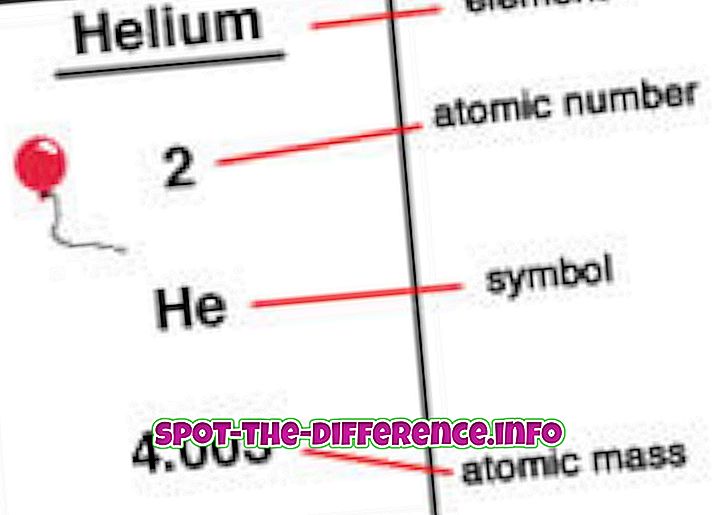
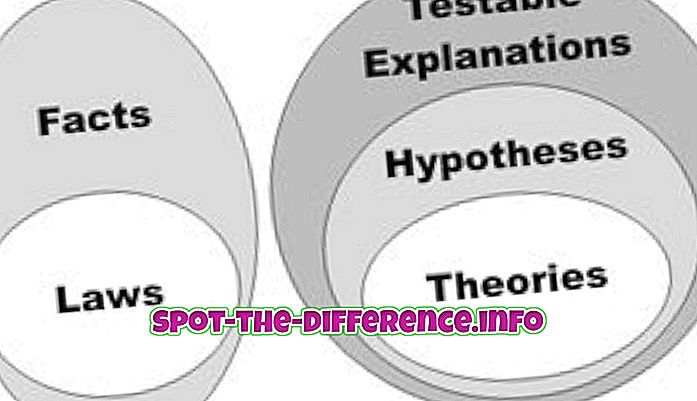
Keskeinen ero: Matematiikassa käytetään yhtälöä kahden ilmaisun välisen tasa-arvon osoittamiseksi. Toisaalta funktio on paljon monimutkaisempi kuin yhtälö. Toimintoa käytetään merkitsemaan tulojen joukon ja vastaavien lähtöjen joukon välistä suhdetta.

Yhtälö ja funktio ovat kaksi algebran perusasemaa, matematiikan alaa. Molemmat voivat olla luonteeltaan varsin monimutkaisia, mutta niiden perusmuodossa niitä voidaan sekoittaa keskenään. Yhtälön ja funktion pääasiallinen ero on se, että yhtälö käsittelee yleensä yhtä tuloa, kun taas funktiolla voi olla lukuisia tuloja.

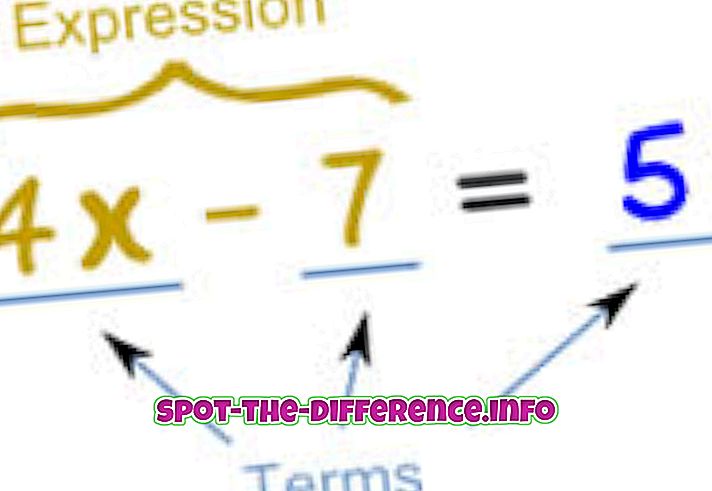
Matematiikassa yhtälöä käytetään ilmaisemaan kahden ilmaisun välistä tasa-arvoa. Pohjimmiltaan yhtälö kirjoitetaan ilmaisuna, joka vastaa toista lauseketta. Esimerkiksi: x + 2 = 5. Tämä tarkoittaa sitä, että mikä tahansa on x, jos lisäät siihen 2, on yhtä suuri kuin 5. Näin ollen voimme ratkaista yhtälön x: lle, joka on 3, 3 + 2 = 5.

Yhtälöt voivat olla monimutkaisempia kuin ne, ja ne voivat sisältää useamman kuin yhden muuttujan, kuten x, y, z jne. Yhdellä yhtälöllä. Esimerkiksi: 3x + 2y - z = 4. Kuitenkin kukin aakkoset vastaa yhtä numeroa. Tässä tapauksessa x = 1, y = 2 ja z = 3.

Siten,

3x + 2y - z = 4 tulee

3 (1) + 2 (2) - 3 = 4, joka on

3 + 4 - 3 = 4 olennaisesti

4 = 4

Toisaalta funktio on paljon monimutkaisempi kuin yhtälö. Toimintoa käytetään merkitsemaan tulojen joukon ja vastaavien lähtöjen joukon välistä suhdetta. Pohjimmiltaan tulon pitäisi antaa yksi lähtö. Funktio on kahden muuttujan välinen suhde. Esimerkiksi: f (x) = x + 2. Tämän toiminnon mukaan, mikä tahansa tulo on, se antaa sinulle yhden lähdön, joka on tulo plus 2. Ratkaistaan ​​tämä toiminto:

panos	Toimia	ulostulo
x	f (x) = x + 2	f (x)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

Ja niin edelleen…

Toiminnoilla on erilaisia ​​sovelluksia matematiikassa, fysiikassa, tietojenkäsittelytieteessä jne. Ne voivat vaihdella yksinkertaisesta funktiosta, kuten edellä on mainittu, monimutkaisiin kaavoihin tai algoritmeihin. Funktiona voidaan ajatella koneena, joka antaa lähtöön tulon, ja että lähtö on jotenkin liittyvä tuloon.

Toiminnossa on aina kolme osaa: tulo, suhde ja lähtö. Klassinen tapa kirjoittaa toiminto on "f (x) = ...", jossa x merkitsee tuloa ja f (x) merkitsee lähtöä.

Kuten edellä on todettu, yhtälön ja funktion välinen pääasiallinen ero on, että yhtälöllä on yleensä vain yksi tulo, joka antaa johtaa lausekkeiden olevan yhtä suuria. Toiminnolla on erilaisia ​​tuloja, joista jokainen antaa ulostulon.